特勒根定理适用范围-特勒根定理适用于什么电路

此定理对任何具有线性非线性时不变时变元件的集总电路都适用，它实质上是电路功率守恒的数学表达式。

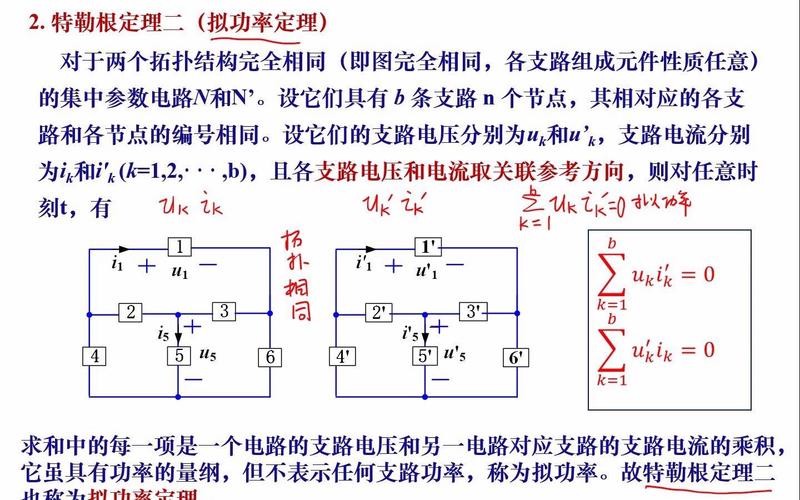
01=bkkkiu01=bkk特勒根定理，于1952年由伯纳德特勒根提出，是电路网络分析理论中最重要的理论之一勒根定理适用于电路网络，只要该网络满足总电流守恒且所有闭合回路电压代数和为零。

应用特勒根定理可方便地证明电路中的互易定理复功率平衡定理等特勒根定理1明确反映了电路实际功率的守恒但特勒根定理2曾仅仅被认为只有功率守恒的数学形式，却无法与实际电路对应，因此定理2也被称为“拟功率定理” 定理2后也被证明反映了电路实际功率的守恒 ，并具有共轭性。

应用特勒根定理在电路分析中有着广泛的应用它可以方便地证明电路中的互易定理复功率平衡定理等此外，特勒根定理还可以用于分析复杂电路中的功率流动和能量转换等问题综上所述，特勒根定理是电路分析中的一个重要定理，它揭示了电路中电流电压和功率之间的平衡关系，为电路的分析和设计提供了有。

电路原理中的补偿定理，也被称为特勒根定理，是电路理论中的一个基本原理这个定理表明，在一个线性时不变集总参数的电阻性电路中，任意两个不同工作状态下，各个支路电压与电流的乘积之和等于零简单来说，它描述了在一定条件下，电路中能量守恒的关系补偿定理的一个重要应用是计算复杂电路中。

定理的扩展进一步丰富了其应用范围，包括任意时刻的能量守恒和电容电感元件的适用当涉及电容或电感时，定理需满足KVL和KCL等电路基本定律，确保能量传递符合电压与电流的关系，以避免因电磁波辐射导致的表面不正确特勒根定理的扩展还包括与电磁场的对应关系，电路分析与电磁场的无散度有旋度场理论相。

3特勒根定理2 如果有两个具有n个结点和b条支路的电路，它们具有相同的图，但由内容不同的支路构成假设各支路电流和电压都取关联参考方向，并分别用I1，I2，···，IbU1，U2，···，Ub和ǐ1，ǐ2，···，ǐbǔ1ǔ2···，ǔb表示两电路中b条支路的电流和电压。

特勒根定理的扩展1表明，该定理适用于电路中的任何元件，包括电容和电感，且任意时刻都满足能量守恒条件因此，特勒根定理任何时刻都正确扩展2说明，当电路包含电容电感等元件时，特勒根定理同样适用，前提是满足KVL和KCL条件能量传递依据电压与电流，电容和电感可能以电磁波形式辐射能量，但可通过增加。

例如，在图1中，我们可以计算出电流值在图2中，我们只是将输入和输出调换位置，且电压源的极性反转因此，注意输出的极性也应相反由于此时是关联参考方向，输出为正因此，图2中的i1应与图1中的i2相同，均为83A我们实际计算一下，结果也是一样的特勒根定理定义简单来说，就是元件。

这个定理用法如下1给定多端口网络的S参数矩阵，其中Sij表示从端口j输入信号到端口i输出信号的传输系数2构造一个NxN的伴随矩阵A，其中N为端口数，Aij=1^i+j*Mij，其中Mij为去掉第i行和第j列后的矩阵的行列式3计算S参数矩阵的行列式D，D=detS，计算特勒根矩阵T，T=AD4。

当讨论直流稳态电路时，互易定理可以顺利应用，因为它简化了问题，使得电路分析仅涉及端口变量的代数运算然而，对于含有动态元件的正弦稳态电路，经典分析方法采用相量法相量法通过选取出代表正弦量的直流当量，并结合初相位，将电路分析转化为复数平面内的运算在正弦稳态电路中，特勒根定理依然适用，因为。

互易定理是由特勒根定理推导出来的，能用互易定理做的都可以用特勒根定理做因为互易定理有三种形式容易记混，所以推荐都用特勒根定理做不容易出错。

在独立源置零后，这两个电路的拓扑图是一样的，都是左侧端口开路，右侧端口短路。

易记的互易定理指南解开电路求解的秘密武器 在电路分析的世界中，特勒根定理就像一盏明灯，引领我们探索互易定理的奥秘这个看似复杂但实际上易于掌握的理论，为求解电路问题带来了极大便利下面，我们将深入解析互易定理的三种表现形式，以及如何记忆和在实际问题中应用基本原理与注意事项对于仅含线性电阻。

电路定理，在线性电路中，任一支路的电流或电压是电路中各个独立源分别作用时在该支路中产生的电流或电压的代数和电路定理分别包括叠加定理替代定理戴维南定理诺顿定理最大传输定理特勒根定理互易定理对偶原理叠加定理陈述及其解释性证明 1定理陈述在线性电路中，任一支路的电流或。

电路定理 电路定理包括叠加定理替代定理戴维南定理诺顿定理特勒根定理和互易定理叠加定理适用于线性时不变系统，替代定理适用于描述端口特性的电压和电流戴维南定理和诺顿定理用于简化电路结构特勒根定理和互易定理是基于功率守恒的推论运算放大器电路 运算放大器电路处理时需要了解其输入阻抗特别。

u1的方向定义为上正下负，is的方向定义为自下而上，两者为非关联方向，因为关联方向的定义是电压电流同向。